已知关于 $x$ 的方程:
$$
p\cdot e^{-x}+q\cdot \sin (x)+r\cdot \cos (x)+s\cdot \tan (x)+t\cdot x^{2}+u=0
$$
其中,$-20\leq q,s,t\leq 0\leq p,r\leq 20$。求这个方程在 $[0,1]$ 内的解,精准到小数点后 $4$ 位。如果无解,输出 No solution。
因为 $q,s,t\leq 0\leq p,r$,所以 $f_{1}(x)=p\cdot e^{-x},f_{2}(x)=q\cdot \sin (x),f_{3}(x)=r\cdot \cos (x),f_{4}(x)=s\cdot \tan (x),f_{5}(x)=t\cdot x^{2}$ 在 $[0,1]$ 范围内单调不增。
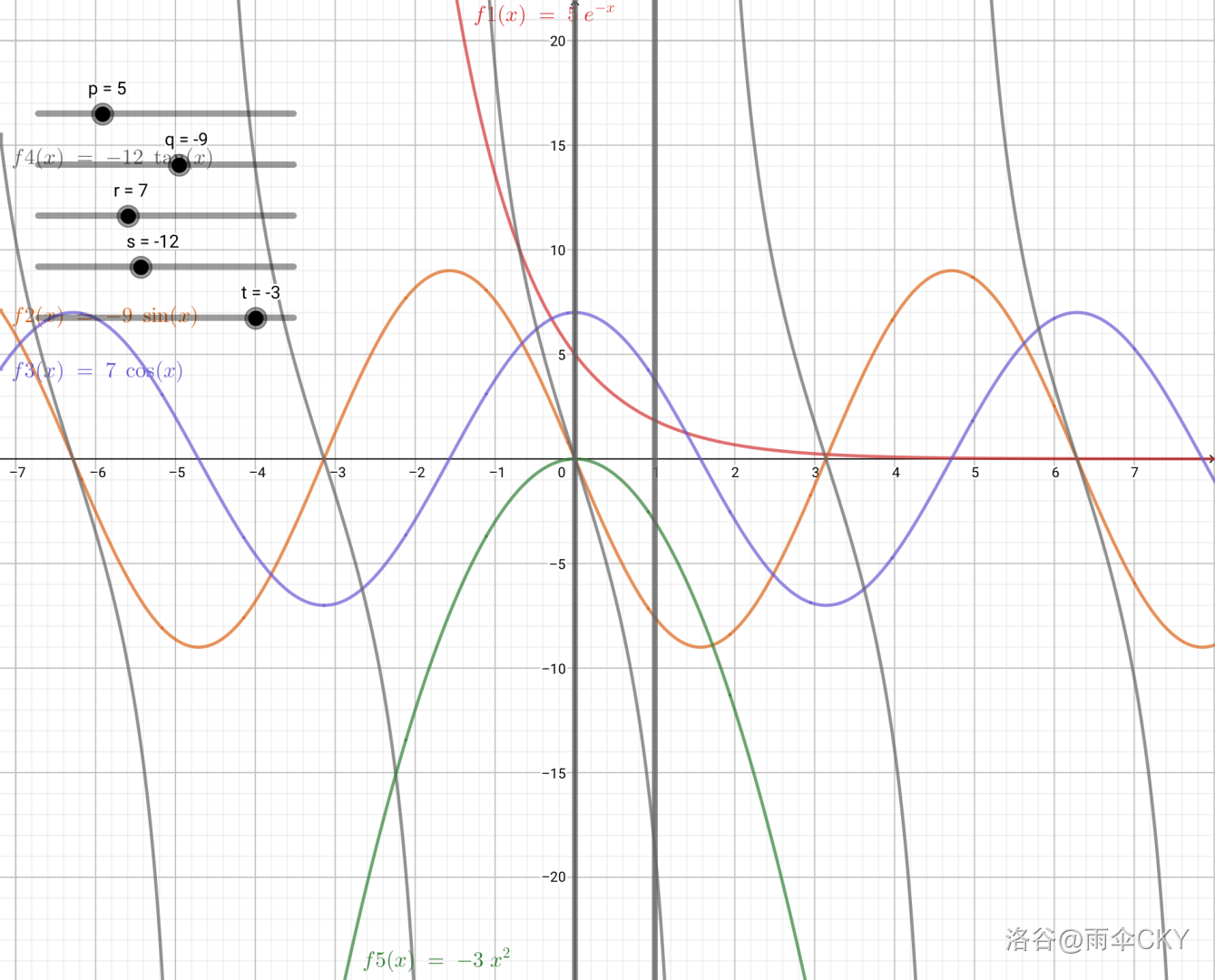
所以它们的和 $f(x)=p\cdot e^{-x}+q\cdot \sin (x)+r\cdot \cos (x)+s\cdot \tan (x)+t\cdot x^{2}$ 也在 $[0,1]$ 范围内单调不增。例如,下图为符合题意的一个随机的 $f(x)$(生成下图的 Python 源码)。
因为函数单调不增,我们可以使用二分查找的方法查找得到答案。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
| #include <cmath>
#include <cstdio>
using namespace std;
double p,q,r,s,t,u,left,right,mid,tmp;
double f(double x){
return p * exp(-x) + q * sin(x) + r * cos(x) + s * tan(x) + t * pow(x,2) + u;
}
int main(){
while (scanf("%lf%lf%lf%lf%lf%lf",&p,&q,&r,&s,&t,&u) != EOF){
left = (double)0,right = (double)1;
for (int i = 1;i <= 50;i++){
mid = (left + right) / (double)2;
tmp = f(mid);
if (fabs(tmp) < 0.00000001) break;
else if (tmp > (double)0) left = mid;
else right = mid;
}
if (fabs(f(mid)) < 0.00000001) printf("%.4lf\n",mid);
else printf("No solution\n");
}
return 0;
}
|

